PEtab import and yaml2sbml
PEtab is a format for specifying parameter estimation problems in systems biology. This notebook illustrates how the PEtab format can be used together with the ODE simulation toolbox AMICI to define ODE based parameter estimation problems for pyABC. Then, in pyABC we can perform exact sampling based on the algorithms introduced in this preprint.
To use this functionality, you need to have (at least) PEtab and AMICI installed. Further, this notebook uses yaml2sbml. You can install all via:
pip install pyabc[petab,amici,yaml2sbml]
AMICI may require some external dependencies.
[ ]:
# install if not done yet
!pip install pyabc[petab,amici,yaml2sbml] --quiet
[1]:
import os
import sys
import amici.petab_import
import matplotlib.pyplot as plt
import numpy as np
import pyabc
import pyabc.petab
%matplotlib inline
pyabc.settings.set_figure_params('pyabc') # for beautified plots
# folders
dir_in = 'models/'
dir_out = 'out/'
os.makedirs(dir_out, exist_ok=True)
Generate PEtab problem from YAML
In this section, we use the tool yaml2sbml to generate a PEtab problem based on a simple human-editable YAML file stored under dir_in, combining it with “measurement” data as generated in a later section. yaml2sbml is a simple way of manually generating models. The PEtab import below works independent of it with any valid PEtab model. We use the common conversion reaction toy model, inferring one parameter and the noise standard variation.
[2]:
import shutil
import petab
import yaml2sbml
# check yaml file
model_name = 'cr'
yaml_file = dir_in + model_name + '.yml'
yaml2sbml.validate_yaml(yaml_file)
YAML file is valid ✅
The format allows to compactly define ODEs, parameters, observables and conditions:
[3]:
with open(yaml_file) as f:
print(f.read())
odes:
- stateId: x1
rightHandSide: (- theta1 * x1 + theta2 * x2)
initialValue: 1
- stateId: x2
rightHandSide: (theta1 * x1 - theta2 * x2)
initialValue: 0
parameters:
- parameterId: theta1
parameterName: $\theta_1$
nominalValue: 0.08
parameterScale: lin
lowerBound: 0.05
upperBound: 0.12
estimate: 1
- parameterId: theta2
parameterName: $\theta_2$
nominalValue: 0.12
parameterScale: lin
lowerBound: 0.05
upperBound: 0.2
estimate: 0
- parameterId: sigma
parameterName: $\sigma$
nominalValue: 0.02
parameterScale: log10
lowerBound: 0.002
upperBound: 1
estimate: 1
observables:
- observableId: obs_x2
observableFormula: x2
observableTransformation: lin
noiseFormula: noiseParameter1_obs_x2
noiseDistribution: normal
conditions:
- conditionId: condition1
We combine the YAML model with “measurement” data (which can be generated as in a later section) to create a PEtab problem. This generates a stand-alone PEtab folder under dir_out.
[4]:
# convert to petab
petab_dir = dir_out + model_name + '_petab/'
measurement_file = model_name + '_measurement_table.tsv'
yaml2sbml.yaml2petab(
yaml_file,
output_dir=petab_dir,
sbml_name=model_name,
petab_yaml_name='cr_petab.yml',
measurement_table_name=measurement_file,
)
# copy measurement table over
_ = shutil.copyfile(dir_in + measurement_file, petab_dir + measurement_file)
petab_yaml_file = petab_dir + 'cr_petab.yml'
# check petab files
!petablint -v -y $petab_yaml_file
Checking SBML model...
Checking measurement table...
Checking condition table...
Checking observable table...
Checking parameter table...
PEtab format check completed successfully.
Import PEtab problem to AMICI and pyABC
We read the PEtab problem, create an AMICI model and then import the full problem in pyABC:
[5]:
# read the petab problem from yaml
petab_problem = petab.Problem.from_yaml(petab_yaml_file)
# compile the petab problem to an AMICI ODE model
amici_dir = dir_out + model_name + '_amici'
if amici_dir not in sys.path:
sys.path.insert(0, os.path.abspath(amici_dir))
model = amici.petab_import.import_petab_problem(
petab_problem,
model_output_dir=amici_dir,
verbose=False,
generate_sensitivity_code=False,
)
# the solver to numerically solve the ODE
solver = model.getSolver()
# import everything to pyABC
importer = pyabc.petab.AmiciPetabImporter(petab_problem, model, solver)
# extract what we need from the importer
prior = importer.create_prior()
model = importer.create_model()
kernel = importer.create_kernel()
Once everything has been compiled and imported, we can simply call the model. By default, this only returns the log likelihood value. If also simulated data are to be returned (and stored in the pyABC datastore), pass return_simulations=True to the importer. return_rdatas returns the full AMICI data objects including states, observables, and debugging information.
[6]:
print(model(importer.get_nominal_parameters()))
{'llh': 22.37843729780134}
We can inspect the prior to see what parameters we infer:
[7]:
print(prior)
<Distribution
theta1=<RV name=uniform, args=(), kwargs={'loc': 0.05, 'scale': 0.06999999999999999}>,
sigma=<RV name=uniform, args=(), kwargs={'loc': -2.6989700043360187, 'scale': 2.6989700043360187}>>
Run analysis with exact inference
Now we can run an analysis using pyABC’s exact sequential sampler under the assumption of measurement noise. For details on the method check the noise assessment notebook. If instead standard distance-based ABC is to be used, the distance function must currently be manually defined from the model output. Here we use a population size of 100, usually a far large size would be preferable.
[8]:
sampler = pyabc.MulticoreEvalParallelSampler()
temperature = pyabc.Temperature()
acceptor = pyabc.StochasticAcceptor()
abc = pyabc.ABCSMC(
model,
prior,
kernel,
eps=temperature,
acceptor=acceptor,
sampler=sampler,
population_size=100,
)
# AMICI knows the data, thus we don't pass them here
abc.new(pyabc.create_sqlite_db_id(), {})
h = abc.run()
ABC.Sampler INFO: Parallelize sampling on 4 processes.
ABC.History INFO: Start <ABCSMC id=2, start_time=2021-12-07 14:17:45>
ABC INFO: Calibration sample t = -1.
ABC.Population INFO: Recording also rejected particles: True
ABC.Population INFO: Recording also rejected particles: True
ABC INFO: t: 0, eps: 1.54589326e+01.
ABC INFO: Accepted: 100 / 375 = 2.6667e-01, ESS: 9.9990e+01.
ABC INFO: t: 1, eps: 7.72946632e+00.
ABC INFO: Accepted: 100 / 439 = 2.2779e-01, ESS: 6.1330e+01.
ABC INFO: t: 2, eps: 3.86473316e+00.
ABC INFO: Accepted: 100 / 617 = 1.6207e-01, ESS: 9.1263e+01.
ABC INFO: t: 3, eps: 1.93236658e+00.
ABC INFO: Accepted: 100 / 568 = 1.7606e-01, ESS: 8.1187e+01.
ABC INFO: t: 4, eps: 1.00000000e+00.
ABC INFO: Accepted: 100 / 479 = 2.0877e-01, ESS: 9.0495e+01.
ABC INFO: Stop: Minimum epsilon.
ABC.History INFO: Done <ABCSMC id=2, duration=0:01:20.515216, end_time=2021-12-07 14:19:06>
That’s it! Now we can visualize our results.
[9]:
pyabc.visualization.plot_kde_matrix_highlevel(
h,
limits=importer.get_bounds(),
refval=importer.get_nominal_parameters(),
refval_color='grey',
names=importer.get_parameter_names(),
);
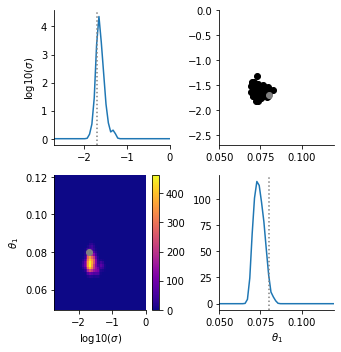
Generate data
This section needs only be run if one wants to generate new synthetic data:
[10]:
# Change this line to run the code
if False:
import importlib
import sys
import amici
import amici.petab_import
import pandas as pd
# check yaml file
model_name = 'cr_base'
yaml_file = dir_in + model_name + '.yml'
yaml2sbml.validate_yaml(yaml_file)
# convert to sbml
sbml_file = dir_out + model_name + '.xml'
yaml2sbml.yaml2sbml(yaml_file, sbml_file)
# convert to amici
amici_dir = dir_out + model_name + '_amici/'
sbml_importer = amici.SbmlImporter(sbml_file)
sbml_importer.sbml2amici(model_name, amici_dir)
# import model
if amici_dir not in sys.path:
sys.path.insert(0, os.path.abspath(amici_dir))
model_module = importlib.import_module(model_name)
model = model_module.getModel()
solver = model.getSolver()
# measurement times
n_time = 10
meas_times = np.linspace(0, 10, n_time)
model.setTimepoints(meas_times)
# simulate with nominal parameters
rdata = amici.runAmiciSimulation(model, solver)
# create noisy data
np.random.seed(2)
sigma = 0.02
obs_x2 = rdata['x'][:, 1] + sigma * np.random.randn(n_time)
obs_x2
# to measurement dataframe
df = pd.DataFrame(
{
'observableId': 'obs_x2',
'simulationConditionId': 'condition1',
'measurement': obs_x2,
'time': meas_times,
'noiseParameters': 'sigma',
}
)
# store data
df.to_csv(
dir_in + model_name[:-5] + '_measurement_table.tsv',
sep='\t',
index=False,
)