Markov jump process: Reaction network
In the following, we fit stochastic chemical reaction kinetics with pyABC and show how to perform model selection between two competing models.
This notebook can be downloaded here: Markov Jump Process: Reaction Network.
We consider the two Markov jump process models \(m_1\) and \(m_2\) for conversion of (chemical) species \(X\) to species \(Y\):
Each model is equipped with a single rate parameter \(k\). To simulate these models, we define a simple Gillespie simulator:
[ ]:
# install if not done yet
!pip install pyabc --quiet
[1]:
import numpy as np
def h(x, pre, c):
return (x**pre).prod(1) * c
def gillespie(x, c, pre, post, max_t):
"""
Gillespie simulation
Parameters
----------
x: 1D array of size n_species
The initial numbers.
c: 1D array of size n_reactions
The reaction rates.
pre: array of size n_reactions x n_species
What is to be consumed.
post: array of size n_reactions x n_species
What is to be produced
max_t: int
Timulate up to time max_t
Returns
-------
t, X: 1d array, 2d array
t: The time points.
X: The history of the species.
``X.shape == (t.size, x.size)``
"""
t = 0
t_store = [t]
x_store = [x.copy()]
S = post - pre
while t < max_t:
h_vec = h(x, pre, c)
h0 = h_vec.sum()
if h0 == 0:
break
delta_t = np.random.exponential(1 / h0)
# no reaction can occur any more
if not np.isfinite(delta_t):
t_store.append(max_t)
x_store.append(x)
break
reaction = np.random.choice(c.size, p=h_vec / h0)
t = t + delta_t
x = x + S[reaction]
t_store.append(t)
x_store.append(x)
return np.array(t_store), np.array(x_store)
Next, we define the models in terms of ther initial molecule numbers \(x_0\), an array pre which determines what is to be consumed (the left hand side of the reaction equations) and an array post which determines what is to be produced (the right hand side of the reaction equations). Moreover, we define that the simulation time should not exceed MAX_T seconds.
Model 1 starts with initial concentrations \(X=40\) and \(Y=3\). The reaction \(X + Y \rightarrow 2Y\) is encoded in pre = [[1, 1]] and post = [[0, 2]].
[2]:
MAX_T = 0.1
class Model1:
__name__ = "Model 1"
x0 = np.array([40, 3]) # Initial molecule numbers
pre = np.array([[1, 1]], dtype=int)
post = np.array([[0, 2]])
def __call__(self, par):
t, X = gillespie(
self.x0, np.array([float(par["rate"])]), self.pre, self.post, MAX_T
)
return {"t": t, "X": X}
Model 2 inherits the initial concentration from model 1. The reaction \(X \rightarrow Y\) is incoded in pre = [[1, 0]] and post = [[0, 1]].
[3]:
class Model2(Model1):
__name__ = "Model 2"
pre = np.array([[1, 0]], dtype=int)
post = np.array([[0, 1]])
We draw one stochastic simulation from model 1 (the “Observation”) and and one from model 2 (the “Competition”) and visualize both
[4]:
%matplotlib inline
import matplotlib.pyplot as plt
true_rate = 2.3
observations = [Model1()({"rate": true_rate}), Model2()({"rate": 30})]
fig, axes = plt.subplots(ncols=2)
fig.set_size_inches((12, 4))
for ax, title, obs in zip(axes, ["Observation", "Competition"], observations):
ax.step(obs["t"], obs["X"])
ax.legend(["Species X", "Species Y"])
ax.set_xlabel("Time")
ax.set_ylabel("Concentration")
ax.set_title(title);
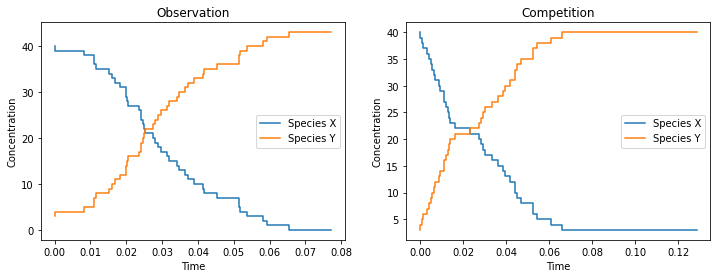
We observe that species \(X\) is converted into species \(Y\) in both cases. The difference of the concentrations over time can be quite subtle.
We define a distance function as \(L_1\) norm of two trajectories, evaluated at 20 time points:
Note that we only consider the concentration of species \(Y\) for distance calculation. And in code:
[5]:
N_TEST_TIMES = 20
t_test_times = np.linspace(0, MAX_T, N_TEST_TIMES)
def distance(x, y):
xt_ind = np.searchsorted(x["t"], t_test_times) - 1
yt_ind = np.searchsorted(y["t"], t_test_times) - 1
error = (
np.absolute(x["X"][:, 1][xt_ind] - y["X"][:, 1][yt_ind]).sum()
/ t_test_times.size
)
return error
For ABC, we choose for both models a uniform prior over the interval \([0, 100]\) for their single rate parameters:
[6]:
from pyabc import RV, Distribution
prior = Distribution(rate=RV("uniform", 0, 100))
We initialize the ABCSMC class passing the two models, their priors and the distance function.
[7]:
from pyabc import ABCSMC
from pyabc.populationstrategy import AdaptivePopulationSize
abc = ABCSMC(
[Model1(), Model2()],
[prior, prior],
distance,
population_size=AdaptivePopulationSize(500, 0.15),
)
INFO:Sampler:Parallelizing the sampling on 4 cores.
We initialize a new ABC run, taking as observed data the one generated by model 1. The ABC run is to be stored in the sqlite database located at /tmp/mjp.db.
[8]:
abc_id = abc.new("sqlite:////tmp/mjp.db", observations[0])
INFO:History:Start <ABCSMC(id=1, start_time=2020-05-17 19:12:20.087395, end_time=None)>
We start pyABC which automatically parallelizes across all available cores.
[9]:
history = abc.run(minimum_epsilon=0.7, max_nr_populations=15)
INFO:ABC:Calibration sample before t=0.
INFO:Epsilon:initial epsilon is 10.65
INFO:ABC:t: 0, eps: 10.65.
INFO:ABC:Acceptance rate: 500 / 1023 = 4.8876e-01, ESS=5.0000e+02.
INFO:Adaptation:Change nr particles 500 -> 115
INFO:ABC:t: 1, eps: 6.75.
INFO:ABC:Acceptance rate: 115 / 272 = 4.2279e-01, ESS=1.0816e+02.
INFO:Adaptation:Change nr particles 115 -> 89
INFO:ABC:t: 2, eps: 5.316484503773134.
INFO:ABC:Acceptance rate: 89 / 167 = 5.3293e-01, ESS=6.2536e+01.
INFO:Adaptation:Change nr particles 89 -> 82
INFO:ABC:t: 3, eps: 3.9215865820412024.
INFO:ABC:Acceptance rate: 82 / 220 = 3.7273e-01, ESS=5.8737e+01.
INFO:Adaptation:Change nr particles 82 -> 92
INFO:ABC:t: 4, eps: 3.2.
INFO:ABC:Acceptance rate: 92 / 330 = 2.7879e-01, ESS=2.1439e+01.
INFO:Adaptation:Change nr particles 92 -> 75
INFO:ABC:t: 5, eps: 2.45.
INFO:ABC:Acceptance rate: 75 / 401 = 1.8703e-01, ESS=2.1633e+01.
INFO:Adaptation:Change nr particles 75 -> 96
INFO:ABC:t: 6, eps: 2.145736215699017.
INFO:ABC:Acceptance rate: 96 / 549 = 1.7486e-01, ESS=2.9474e+01.
INFO:Adaptation:Change nr particles 96 -> 102
INFO:ABC:t: 7, eps: 1.75.
INFO:ABC:Acceptance rate: 102 / 792 = 1.2879e-01, ESS=7.8885e+01.
INFO:Adaptation:Change nr particles 102 -> 58
INFO:ABC:t: 8, eps: 1.4.
INFO:ABC:Acceptance rate: 58 / 357 = 1.6246e-01, ESS=4.9798e+01.
INFO:Adaptation:Change nr particles 58 -> 57
INFO:ABC:t: 9, eps: 1.25.
INFO:ABC:Acceptance rate: 57 / 583 = 9.7770e-02, ESS=4.1186e+01.
INFO:Adaptation:Change nr particles 57 -> 61
INFO:ABC:t: 10, eps: 1.0627609318694404.
INFO:ABC:Acceptance rate: 61 / 1185 = 5.1477e-02, ESS=5.7597e+01.
INFO:Adaptation:Change nr particles 61 -> 46
INFO:ABC:t: 11, eps: 0.95.
INFO:ABC:Acceptance rate: 46 / 1461 = 3.1485e-02, ESS=4.2846e+01.
INFO:Adaptation:Change nr particles 46 -> 52
INFO:ABC:t: 12, eps: 0.8.
INFO:ABC:Acceptance rate: 52 / 4317 = 1.2045e-02, ESS=3.9330e+01.
INFO:Adaptation:Change nr particles 52 -> 53
INFO:ABC:t: 13, eps: 0.75.
INFO:ABC:Acceptance rate: 53 / 4867 = 1.0890e-02, ESS=4.8614e+01.
INFO:Adaptation:Change nr particles 53 -> 51
INFO:ABC:t: 14, eps: 0.6526353965182403.
INFO:ABC:Acceptance rate: 51 / 15746 = 3.2389e-03, ESS=4.4594e+01.
INFO:Adaptation:Change nr particles 51 -> 55
INFO:ABC:Stopping: minimum epsilon.
INFO:History:Done <ABCSMC(id=1, start_time=2020-05-17 19:12:20.087395, end_time=2020-05-17 19:14:05.753541)>
We first inspect the model probabilities.
[10]:
ax = history.get_model_probabilities().plot.bar()
ax.set_ylabel("Probability")
ax.set_xlabel("Generation")
ax.legend(
[1, 2], title="Model", ncol=2, loc="lower center", bbox_to_anchor=(0.5, 1)
);
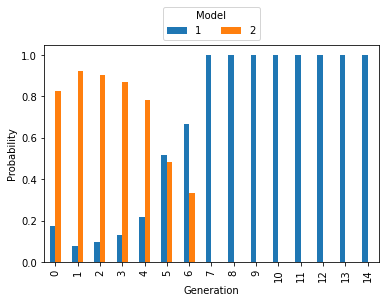
The mass at model 2 decreased, the mass at model 1 increased slowly. The correct model 1 is detected towards the later generations. We then inspect the distribution of the rate parameters:
[11]:
from pyabc.visualization import plot_kde_1d
fig, axes = plt.subplots(2)
fig.set_size_inches((6, 6))
axes = axes.flatten()
axes[0].axvline(true_rate, color="black", linestyle="dotted")
for m, ax in enumerate(axes):
for t in range(0, history.n_populations, 2):
df, w = history.get_distribution(m=m, t=t)
if len(w) > 0: # Particles in a model might die out
plot_kde_1d(
df,
w,
"rate",
ax=ax,
label=f"t={t}",
xmin=0,
xmax=20 if m == 0 else 100,
numx=200,
)
ax.set_title(f"Model {m+1}")
axes[0].legend(title="Generation", loc="upper left", bbox_to_anchor=(1, 1))
fig.tight_layout()
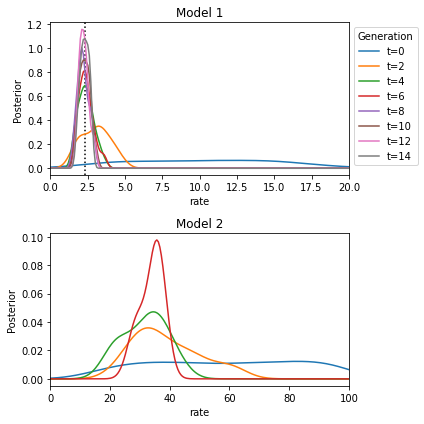
The true rate is closely approximated by the posterior over the rate of model 1. It is a little harder to interpret the posterior over model 2. Apparently a rate between 20 and 40 yields data most similar to the observed data.
Lastly, we visualize the evolution of the population sizes. The population sizes were automatically selected by pyABC and varied over the course of the generations. (We do not plot the size of th first generation, which was set to 500)
[12]:
populations = history.get_all_populations()
ax = populations[populations.t >= 1].plot("t", "particles", style="o-")
ax.set_xlabel("Generation");
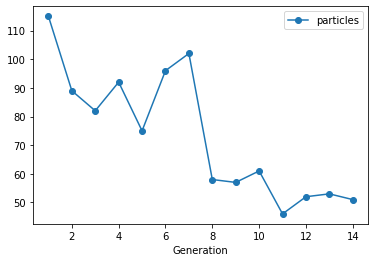
The initially chosen population size was adapted to the desired target accuracy. A larger population size was automatically selected by pyABC while both models were still alive. The population size decreased during the later populations thereby saving computational time.